I decided to finally blog this since I can never frickin remember which is which. Maybe if I write this and draw the diagram it'll finally stick. If not, I'll have something to come back to. To make it more accessible I'll be using a running example: the bike allocation problem. Given a group of people and a set of bikes, who gets which bike?
Partial functions
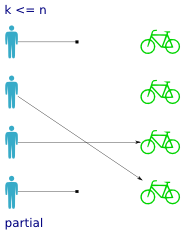 Partial functions are pretty self explanatory. All you have to remember is which side the partiality concerns. In our example a partial function means that not every person has been assigned a bike. Some persons do not have bikes, so
Partial functions are pretty self explanatory. All you have to remember is which side the partiality concerns. In our example a partial function means that not every person has been assigned a bike. Some persons do not have bikes, so lookup_bike(person) will not work on all inputs.
Partial functions are common in code: reading from files that don't exist, and of course the ever lurking NullPointerException -- following a pointer to an object that is not live. In haskell, this is where the Maybe monad appears.
Total functions
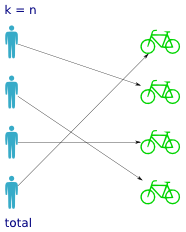 Not surprisingly, total functions are the counterpart to partial functions. A total function has a value for every possible input, so that means every person has been assigned a bike. But it doesn't tell you anything about how the bikes are distributed over the persons; whether it's one-to-one, all persons sharing the same bike etc.
Not surprisingly, total functions are the counterpart to partial functions. A total function has a value for every possible input, so that means every person has been assigned a bike. But it doesn't tell you anything about how the bikes are distributed over the persons; whether it's one-to-one, all persons sharing the same bike etc.
Clearly, total functions are more desirable than partial ones -- it means the caller can call the function with any value without having to check it first. Partial functions often masquerade as total ones, by returning a value outside the expected range (which explains the existence of a null value in just about every programming language and data format). In python the value 0, None and any empty sequence (string, list, tuple, dict) all represent null, which makes writing total functions easy.
Bijective/isomorphic functions (forall one-to-one)
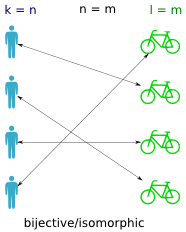 A bijective function (also called isomorphic) is a one-to-one mapping between the persons and the bikes (between the domain and codomain). It means that if you find a bike, you can trace it back to exactly one person, and that if you have a person you can trace it to exactly one bike. In other words it means the inverse function works, that is both
A bijective function (also called isomorphic) is a one-to-one mapping between the persons and the bikes (between the domain and codomain). It means that if you find a bike, you can trace it back to exactly one person, and that if you have a person you can trace it to exactly one bike. In other words it means the inverse function works, that is both lookup_bike(person) and lookup_person(bike) work for all inputs.
Isomorphic functions are found in all kinds of translations; storing objects in a database, compressing files etc. The name literally means "the same shape", so any format that can reproduce the same structure can represent the same data.
Injective functions (one-to-one)
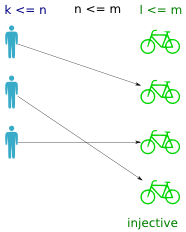 An injective function returns a distinct value for every input. That is, no bike is assigned to more than one person. If the function is total, then what prevents it from being bijective is the unequal cardinality of the domain and codomain (ie. more bikes than persons).
An injective function returns a distinct value for every input. That is, no bike is assigned to more than one person. If the function is total, then what prevents it from being bijective is the unequal cardinality of the domain and codomain (ie. more bikes than persons).
Another way to understand it is to think of something small being stored in (embedded in) something big. In order to maintain unique output values, the codomain must be at least as big as the domain. GUIDs are an example of this. A GUID generator guarantees a globally unique identifier by picking values from a sufficiently large space. Given a GUID that has been issued, you can trace it back to exactly one object, but you cannot take just any value in the GUID space, because most of them have never (and will never) be issued to anyone.
Surjective functions (many-to-one)
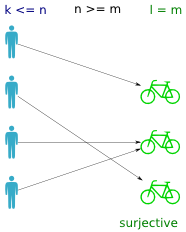 A surjective function is one where all values in the codomain are used (ie. all bikes are assigned). In a way it is the inverse property of a total function (where all persons have a bike).
A surjective function is one where all values in the codomain are used (ie. all bikes are assigned). In a way it is the inverse property of a total function (where all persons have a bike).
Surjective functions are often undesirable in practice, meaning that you have too few resources at your disposal, which forces sharing (threads on a cpu) or rejection (streaming server can only accept so many clients).
The way to think of injections and surjections is not as opposites, but as complementary properties. A function can be both injective (all persons have a unique bike) and surjective (all bikes are used). If so, it is bijective.

 December 2nd, 2012
December 2nd, 2012
 Partial functions are pretty self explanatory. All you have to remember is which side the partiality concerns. In our example a partial function means that not every person has been assigned a bike. Some persons do not have bikes, so
Partial functions are pretty self explanatory. All you have to remember is which side the partiality concerns. In our example a partial function means that not every person has been assigned a bike. Some persons do not have bikes, so  Not surprisingly, total functions are the counterpart to partial functions. A total function has a value for every possible input, so that means every person has been assigned a bike. But it doesn't tell you anything about how the bikes are distributed over the persons; whether it's one-to-one, all persons sharing the same bike etc.
Not surprisingly, total functions are the counterpart to partial functions. A total function has a value for every possible input, so that means every person has been assigned a bike. But it doesn't tell you anything about how the bikes are distributed over the persons; whether it's one-to-one, all persons sharing the same bike etc. A bijective function (also called isomorphic) is a one-to-one mapping between the persons and the bikes (between the domain and codomain). It means that if you find a bike, you can trace it back to exactly one person, and that if you have a person you can trace it to exactly one bike. In other words it means the inverse function works, that is both
A bijective function (also called isomorphic) is a one-to-one mapping between the persons and the bikes (between the domain and codomain). It means that if you find a bike, you can trace it back to exactly one person, and that if you have a person you can trace it to exactly one bike. In other words it means the inverse function works, that is both  An injective function returns a distinct value for every input. That is, no bike is assigned to more than one person. If the function is total, then what prevents it from being bijective is the unequal cardinality of the domain and codomain (ie. more bikes than persons).
An injective function returns a distinct value for every input. That is, no bike is assigned to more than one person. If the function is total, then what prevents it from being bijective is the unequal cardinality of the domain and codomain (ie. more bikes than persons). A surjective function is one where all values in the codomain are used (ie. all bikes are assigned). In a way it is the inverse property of a total function (where all persons have a bike).
A surjective function is one where all values in the codomain are used (ie. all bikes are assigned). In a way it is the inverse property of a total function (where all persons have a bike).