May 24th, 2009
I decided to finally blog this since I can never frickin remember which is which. Maybe if I write this and draw the diagram it'll finally stick. If not, I'll have something to come back to. To make it more accessible I'll be using a running example: the bike allocation problem. Given a group of people and a set of bikes, who gets which bike?
Partial functions
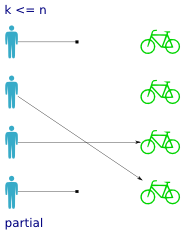Partial functions are pretty self explanatory. All you have to remember is which side the partiality concerns. In our example a partial function means that not every person has been assigned a bike. Some persons do not have bikes, so lookup_bike(person) will not work on all inputs.
Partial functions are common in code: reading from files that don't exist, and of course the ever lurking NullPointerException -- following a pointer to an object that is not live. In haskell, this is where the Maybe monad appears.
Total functions
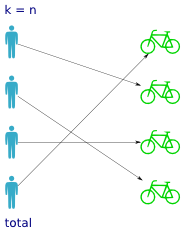Not surprisingly, total functions are the counterpart to partial functions. A total function has a value for every possible input, so that means every person has been assigned a bike. But it doesn't tell you anything about how the bikes are distributed over the persons; whether it's one-to-one, all persons sharing the same bike etc.
Clearly, total functions are more desirable than partial ones -- it means the caller can call the function with any value without having to check it first. Partial functions often masquerade as total ones, by returning a value outside the expected range (which explains the existence of a null value in just about every programming language and data format). In python the value 0, None and any empty sequence (string, list, tuple, dict) all represent null, which makes writing total functions easy.
Bijective/isomorphic functions (forall one-to-one)
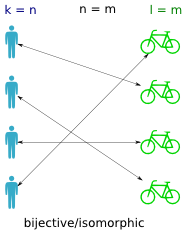A bijective function (also called isomorphic) is a one-to-one mapping between the persons and the bikes (between the domain and codomain). It means that if you find a bike, you can trace it back to exactly one person, and that if you have a person you can trace it to exactly one bike. In other words it means the inverse function works, that is both lookup_bike(person) and lookup_person(bike) work for all inputs.
Isomorphic functions are found in all kinds of translations; storing objects in a database, compressing files etc. The name literally means "the same shape", so any format that can reproduce the same structure can represent the same data.
Injective functions (one-to-one)
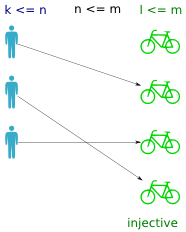An injective function returns a distinct value for every input. That is, no bike is assigned to more than one person. If the function is total, then what prevents it from being bijective is the unequal cardinality of the domain and codomain (ie. more bikes than persons).
Another way to understand it is to think of something small being stored in (embedded in) something big. In order to maintain unique output values, the codomain must be at least as big as the domain. GUIDs are an example of this. A GUID generator guarantees a globally unique identifier by picking values from a sufficiently large space. Given a GUID that has been issued, you can trace it back to exactly one object, but you cannot take just any value in the GUID space, because most of them have never (and will never) be issued to anyone.
Surjective functions (many-to-one)
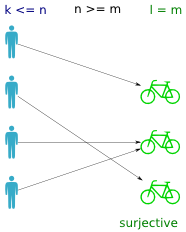A surjective function is one where all values in the codomain are used (ie. all bikes are assigned). In a way it is the inverse property of a total function (where all persons have a bike).
Surjective functions are often undesirable in practice, meaning that you have too few resources at your disposal, which forces sharing (threads on a cpu) or rejection (streaming server can only accept so many clients).
The way to think of injections and surjections is not as opposites, but as complementary properties. A function can be both injective (all persons have a unique bike) and surjective (all bikes are used). If so, it is bijective.
Small nitpick: bijective is not the same as isomorphic. For example, in topological spaces, a bijective continuous function is only an isomorphism if the inverse is also continuous.
I figured someone would bring this up, I know they are not exactly the same but similar. I have no idea what a topological space is, though.
Anyway, for my purposes they are the same, thus far.
In the category of sets bijective is the same as isomorphism. If there is no further structure on the sets (as is the case with people and bikes), then it doesn't matter which term you use.
Well, a map being a bijection is a property that just has to do with sets, whereas a map being an isomorphism is a stronger property: it means that the map is a bijection which also preserves some extra mathematical structure.
Bijections preserve cardinality (size), while isomorphisms preserve structure.
If you only consider things as sets, there is no extra structure to preserve, so any bijection is an isomorphism. But if you consider things with additional mathematical structure, the two are no longer equivalent. For example, it is possible to find a bijection between the real line and the plane. So, considered as sets, they are isomorphic. But considering them as vector spaces, where we can add vectors and scale them, they are not isomorphic, because the real line is one-dimensional and the plane is two-dimensional. Whatever bijection we find between them will not preserve the vector space structure, which is important.
In general, a bijection is defined as a 1-1 onto map, while an isomorphism is defined in abstract algebra as a bijective map that preserves structure. Since sets have no structure, set isomorphisms are indeed bijections. For objects with any sort of additional structure (well-ordered sets, posets, groups, rings, fields, lattices, etc) though, they aren't the same.
Surjective functions find a lot of use as hash functions for hash tables and their variants. Ideally, you'd want every bucket in a table to have some objects assigned to it, therefore the hash function must be designed such that it is surjective.
Also, from a mathematical point of view, partial functions aren't really functions. By definition, a function must map each object in its domain (persons here) to an object in the codomain (bikes). Real life is more interesting though :)
Would you mind sharing with us what your purposes are? Because, for the purposes of the branch of mathematics where these classifications were devised, there obviously IS an important difference.
Just gonna chime in here, it's usually a "partial relation" and not a partial function, since "function" has a very specific meaning, i.e. each item in the left is mapped to AT MOST one item on the right. Additionally, an injective function does not necessarily mean every input has an output. It means that, for those input that DO have an output, that output is unique. What you're describing is a total, injective function.
[...] classes of functionsIf you often get confused by terms like injective, surjective and bijective, this blog post including diagrams and programming analogies should help. [...]
thanks, this helped